I spent 15 years of my life learning a ton of things in math, but there’s only one thing I learned that I still use all the time as a designer.  That’s using ratios and proportions (which I guess is kind of like really basic algebra). If you’re going into the design industry, I can’t stress how much understanding them is going to save you headaches.

Now I’ll admit, Math was one of my better subjects, but I by no means would consider myself good at it.  I use a calculator for most everything.  I promise, I’m going to make learning proportions super easy so that you don’t have to really think about what’s going on.

What are Ratios and Proportions

The basic idea of ratios is to describe parts of the whole or a relationship between things.  A proportion is the process of extracting a ratio into a new form that is mathematically equal to the same original ratio but just looks a little different.

We’ll start simple…

Case A) If you have 1 red squares and 2 blue squares your ratio is 1:2.

Case B) If you have 3 red squares and 6 blue squares your ratio would still be 1:2.

Even though case A & B have different total quantities, their ratio is the same, and so they are directly proportional.

How to Set Ratios and Proportions Up To Solve for an Unknown

If you ever run into case where you know the original ratio of something and but are having trouble finding proportional information, you can always do some basic algebra to solve for the unknown.

Let’s say I’m given a roof slope of 6:12 (rise/run) by an architect.  That means for every vertical 6″ I must also increment 12″ horizontally.

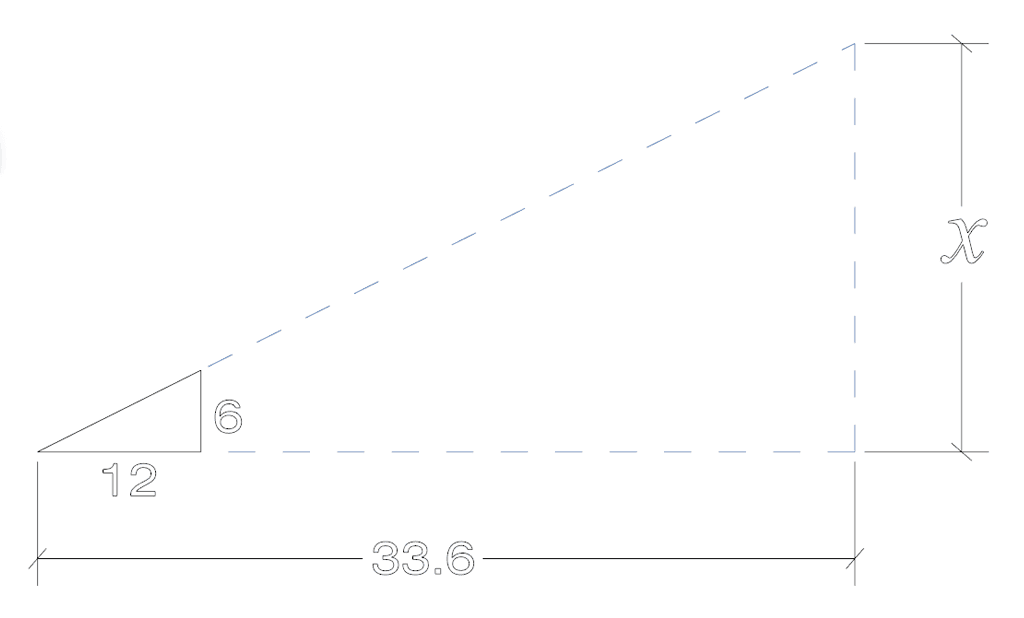
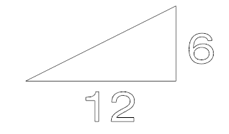I know that from the roof edge to my ridge (the topmost portion of my roof) is 33.6″  but I don’t know the height.  For this, I can use ratios and proportions to solve for the unknown.

We start by turning 6:12 into a fraction. 6/12.  They’re basically the same thing, the ” : ” (colon) is simply a shorthand of letting someone know it’s a ratio to be used proportionally.

We then need to set what our ratio is equal to.  For this we have to keep like items in alignment.  The 12″ run of the ratio is relational to the 33.6 length we already know.  We’ll put those two on the same side of the division line because of that.   In the same idea, 6″ is the rise of our ratio and will be directly proportional to the X rise we intend to find.  We’ll keep both of those on the top of our fractions.

Solving Proportions

If you set up your proportions the way I describe above, you can solve for x pretty easily.  I’ve developed the mnemonic device called MAD to help you remember.

M  ultiply

A  cross

then

D  ivide

What you’re doing when you multiply across and then divide is reworking the equation to solve for x.  Just so you know, I’ve rewritten what it looks like below.  Don’t be alarmed though, you can just follow the above MAD rule and don’t have to worry about knowing the algebra.

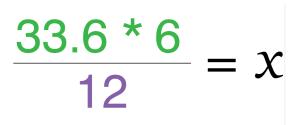
Where Using Proportions is Helpful

I shared a few examples above, but I use proportions in a bunch of ways:

• In programs that don’t allow you to scale to a reference and you need to scale with a percentage or factor
• When a drawing is at a particular scale and you only have a measuring tape
• When you like the way something looks but want to make it larger or smaller to an exact size
• When I want to convert between similar units like miles and yards

What type of things do you use ratios and proportions for?  Leave a comment below!

If you liked this and want to become a part of the design nation, subscribe to our newsletter!